Epílogo para matemáticos

``Me lisonjeo de que las presentes tablas están sin errata alguna, pues habiendo ofrecido cien francos de recompensa por cada una que se me señalare en los logaritmos, no he recibido demanda alguna.'' (J. de Lalande, 1800)

Como vimos, no fué fácil para los cerebros chilenos de la época comprender el significado de una tabla matemática. Tampoco lo es hoy día, en que la microelectrónica mató el romanticismo de los cálculos manuales. Ni siquiera es fácil evaluar la calidad de una de ellas. Menos aún situar la importancia de su mecanismo de cálculo, una tarea que requiere no sólo paciencia, sino también conocimientos matemáticos y gran ingenio.

Las tablas matemáticas son más antiguas de lo que uno sospecha intuitivamente. De hecho la primera tabla, en el sentido moderno del término, de que se tenga registro, data de la mitad del siglo II A.C., y da los valores de las cuerdas de un círculo a intervalos de medio grado con 6 cifras de aproximación. Mas, no es sino en el siglo XV que comienza realmente el desarrollo de las tablas matemáticas en su sentido actual. Podríamos nombrar entre las más conocidas las tablas de senos de Regiomontanus (1490), las tablas de tangentes de Reinhold (1543) y el trabajo de toda la vida de Rheticus (1514-76), una tabla de funciones trigonométricas de 15 cifras decimales para cada 10 segundos de arco, y en cuya construcción se ocuparon varios calculistas y 12 años de trabajo, y que sólo terminó, despues de la muerte del maestro, un alumno suyo, V. Otho. Poco después, en 1614, Napier publicó la primera tabla de logaritmos ampliamente conocida, al tiempo que Briggs calculaba y publicaba en 1624 la primera tabla de logaritmos en base 10. Con esto quedaba abierta la puerta para el uso y cálculo de funciones trigonométricas logarítmicas con el consiguiente alivio de los usuarios de las tablas, particularmente los astrónomos, navegantes y agrimensores.

Un curso similar siguieron las tablas de cuadrados, cubos y raíces. En las de recíprocos, destacan las tablas de Goodwyn y las de Barlow, ambas de comienzos del siglo XIX. Aproximadamente medio siglo después aparecen las tablas de división de Picarte, publicadas en Francia en 1861, que permiten calcular rápidamente por medio de un sencillo algoritmo, el cuociente de dos números con una aproximación de 10 cifras significativas, superando así a las de Goodwyn y también a las de Barlow que sólo dan 7 cifras.

En los días de Picarte, las tablas más conocidas y usadas eran las ``Tablas de logaritmos para los números y los senos'' de J. de La Lande, famoso astrónomo francés. Eran unas tablas de bolsillo de $\log N$ hasta $N=10.000$ y de logaritmos de $\operatorname{sen} x$, $\operatorname{cos} x$, $\operatorname{tan} x$ y $\operatorname{cotan} x$ de minuto en minuto hasta $x=45^{\circ}$. Lalande -hombre de experiencia en estas materias- se refiere así a la forma y tamaño de sus tablas: ``No he puesto más de seis cifras en los logaritmos, porque no se necesita la séptima cuando no se calculan ángulos más que por minutos y los números a 4 guarismos: acerca de lo cual tengo 50 años de experiencia''. El ámbito de aplicaciones de las tablas, según reza la cubierta, era ``Astronomía, la Gnomónica, la Geometría, la Navegación, la Geografía, la Física, el Arte Militar, la Arquitectura, la Agrimensura, la Estadística y las Rentas'' y agrega que ``el primer uso de los logaritmos consiste en abreviar las multiplicaciones y las divisiones, principalmente en las reglas de tres.'' Por otra parte, ``los senos de que se sirven en todas los operaciones de triángulos, bien sea para el cielo, la tierra, para el mar, deben tener también sus logaritmos.'' $^{\arabic{notas}}\,$

Este era el modelo que Picarte y sus compatriotas tenían en mente cuando hablaban de una ``tabla matemática''. Para quien construye la tabla, sin embargo, hay una serie de otros parámetros técnicos a considerar que hacen que una tabla sea buena o mala, útil o inservible:

``El valor intrínseco de una tabla debe ser estimado por la cantidad de tiempo ahorrado al consultarla: por ejemplo, una tabla de raíces cuadradas de diez decimales es más valiosa que una tabla de cuadrados, pues la extracción de raíz ocuparía más tiempo que la multiplicación del número por sí mismo. El valor de una tabla no depende de las dificultades para calcularla: puesto que, una vez hecha, queda para siempre y en lo que respecta al usuario el tiempo ocupado en su construcción es el mismo que si todos los resultados de la tabla hubiesen sido calculados separadamente; pero en la mayoría de los casos una tabla puede ser formada por métodos expeditos que son inaplicables para el cálculo de un resultado individual. Este es el caso de tablas con cantidades continuas, que pueden ser frecuentemente construídas por diferencias. El más impactante caso quizás, es el proporcionado por una tabla de factores o una tabla de primos; pues, si se requiere determinar si un número dado es primo o no, el único método a disposición universalmente (en la ausencia de tablas) es dividirlo por cada primo menor que su raíz cuadrada o hasta que se encuentra uno que lo divide sin resto. Pero para formar una tabla de números primos el proceso es teóricamente simple y rápido, puesto que solamente necesitamos colocar todos los números en una línea, y tarjar los números de dos en dos partiendo de 2, de tres en tres partiendo de 3, y así sucesivamente: los que quedan son los primos. Aun cuando los resultados tabulares sean construídos separadamente, el método de las diferencias u otros métodos que relacionen diferentes resultados tabulares permiten al calculador no sólo ahorrar tiempo y trabajo, sino también obtiene la certeza de exactitud.''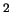 $^{\arabic{notas}}\,$

Se podría indicar como los aspectos centrales a tener en mente a la hora de evaluar matemáticamente una tabla los siguientes:

1. La función que calcula la tabla. No sólo la dificultad de la función, sino su utilidad, su frecuencia de uso.

2. El rango, es decir, el intervalo sobre el cual los valores del argumentos son considerados. Mientras mayor el rango, más valor tiene la tabla.

3. El número de cifras significativas, es decir, el número de cifras que entrega la tabla para cada valor del argumento. A mayor número de cifras significativas, más precisión en el cálculo.

4. ¿Es práctico su uso? Esto depende de la elección de los parámetros, incluso de la forma de presentar visualmente los resultados.

5. La seguridad, es decir, la ausencia de errores.

6. El método usado para calcularla. ¿Es práctico? ¿Permite calcular otras tablas? ¿Se puede generalizar?

Hechas estas consideraciones, nos abocaremos a las tablas de división de Picarte, las más importantes en su tipo --aún hoy día-- que ideó, diseñó y calculó a mediados del siglo XIX. $^{\arabic{notas}}\,$

Bajo el título La Division reduite a un Addition (París, Mallet-Bachelier, 1861), Picarte publica, luego de una calurosa aprobación por la Academia de Ciencias de Francia (ver informe completo en el Apéndice), su tabla clásica sobre recíprocos. Es una tabla muy sencilla, que como lo dice su título, tiene por objetivo reducir la división, ``esa operación larga i penosa'' a una simple suma. Entrega en cada línea los cuocientes $1/n, 2/n, \dots, 9/n$, para cada $n$ desde 1 hasta 10.000, con diez cifras significativas. Supera en este aspecto a la de Barlow que da sólo 7 cifras y nada más que los cuocientes de la forma $1/n$, así como también a la de Goodwyn que entrega $d/n$ para $d < n$ y primos entre sí, y sólo para $n < 1.000$ en lo sustancial. Esto habría bastado para entrar a la galería de calculistas célebres.

Pero esto no es todo ni lo fundamental. La tabla está diseñada --y ésta es su peculiaridad distintiva y original-- para calcular rápidamente, por medio de un sencillo procedimiento, el cuociente de dos números cualesquiera con una aproximación de 10 cifras significativas. Esta es la gran novedad para la época: nadie lo había hecho ni pensado hasta ese entonces. El cuadro adjunto muestra sumariamente el método para calcular una división usando las tablas a través de un ejemplo.

Para los divisores de más de cuatro cifras el método de interpolación usual funciona bien si sólo se desean seis o siete cifras para el cuociente. Si se quieren más, Picarte propone aprovechar la siguiente observación. Si $c= \frac{a}{b}$ y se quiere calcular $x=\frac{a}{b+ n}$, entonces mediante un cálculo elemental se obtiene

$$x = c - \frac{n c}{b+ n}.$$

Usando reiteradamente esta fórmula para $n « b$, no es difícil mostrar que $x$ se puede aproximar con diez cifras significativas como $x \approx c -c_1 +c_2$, donde $c$ es el valor de $\frac{a}{b}$ obtenido de la tabla, $c_1$ es el valor de $\frac{nc}{b}$ obtenido de la tabla, y finalmente $c_2$ es el valor de $\frac{nc_1}{b}$ obtenido de la tabla. Así por ejemplo para $x=674/513922$ usamos $b=513900$ ($5139$ está en la tabla) y $n=22$ para obtener el cuociente de 10 cifras $1311483065$, o sea $x=0,001311483065$.

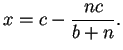
Finalmente daremos una breve idea del algoritmo que Picarte usó para lograr la gran precisión que tienen sus tablas, lo que llevó a Comrie a chequear con ellas la nueva edición de las tablas de Barlow que preparó en 1930. $^{\arabic{notas}}\,$ Picarte parte de la simple identidad

$$\frac{a^2}{b} = (2a - b) + \frac{(a-b)^2}{b}.$$

La observación clave, hace notar Picarte, es que la parte entera de $\frac{a^2}{b}$ es $2a-b$ más la parte entera de $\frac{(a-b)^2}{b}$. Si se aplica esta fórmula a números de la forma $a=10^n$, transformararemos el problema de obtener cifras significativas en el de calcular partes enteras de cuocientes.

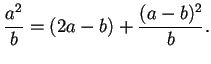
En su primera tabla calculada en Chile, usa esta fórmula para calcular las primeras cinco cifras significativas de los cuocientes. Es decir, aplica la fórmula para $a=10000$; de esta forma, las cinco cifras significativas de $\frac{1}{b}$, para $b$ entero de cinco cifras, serán la parte entera del cuociente $\frac{a^2}{b}$.

A modo de ilustración, veamos algunos casos. Para los divisores entre $9999$ y $9901$ se obtiene que $\frac{(a-b)^2}{b} < 1$, luego la parte entera de $\frac{a^2}{b}$ es exactamente $2a-b$. Para los divisores entre $9900$ y $9860$, la parte entera de $\frac{(a-b)^2}{b}$ es $1$, luego la parte entera de $\frac{a^2}{b}$ es $2a-b+1$. El proceso sigue en forma similar. Usando estos resultados, los cuocientes se pueden obtener contruyendo una tabla que contiene cuatro columnas como se puede apreciar en el cuadro anexo, que se llena mecánicamente de arriba hacia abajo. (Esto explica la ausencia de errores de las tablas de Picarte: un procedimiento sencillo --usa sólo sumas-- para calcular las entradas).

$b$	$(a-b)^2$ o resto de $\frac{(a-b)^2}{b}$	auxiliar	cuociente
9999	1	3	10001
9998	4	5	10002
9997	9	7	10003
9996	16	9	10004
$\vdots$	$\vdots$	$\vdots$	$\vdots$
9902	9604	197	10098
9901	9801	199	10099
9900	100	202	10101
9899	302	204	10102
$\vdots$	$\vdots$	$\vdots$	$\vdots$

Obsérvese que la cantidad auxiliar (números de la forma $2n+1$) se necesita para calcular mecánicamente $(a-b)^2$, debido a la propiedad $(n+1)^2 - n^2 = 2n+1$, es decir el siguiente número cuadrado $(n+1)^2$ se obtiene del anterior $n^2$ sumando $2n+1$. Similarmente para los restos si corresponde.

Usando este procedimiento, Picarte calculó los cuocientes con cinco cifras significativas desde $9999$ hasta $5000$. Para determinar las restante cuatro últimas cifras usó un procedimiento de interpolación junto a ingeniosas observaciones sobre los números del rango considerado.

Finalmente, para los cuocientes correspondientes a $2500 \leq b \leq 4999$, considera los múltiplos de $2$ ( $4999\times 2$, etc.); para los del rango $1250 \leq b \leq 2499$, los múltiplos de cuatro. Por último, desde $1249$ a $1001$, los cuocientes se determinaron directamente.